Maths - Trigonometry - Derived Trig Functions

Double Angle Formula

Since quaternions use expressions like sin(t/2) and cos(t/2) it would be useful to have expressions for these in terms of sin(t) and cos(t)

As a starting point take the following trig functions:

sin(2A) = 2 sin(A) cos(A)

cos(2A) = 2 cos²(A) - 1 = 1 - 2 sin²(A)

where:

• cos²(A) is shorthand notation for (cos(A))², that is, the square of cos
• sin²(A) is shorthand notation for (sin(A))², that is, the square of sine

Half Angle Formula

sin(t/2) =√(0.5 (1- cos(t))) cos(t/2) =√(0.5 (1+ cos(t))) tan(t/2) = sin(t)/(1+cos(t))

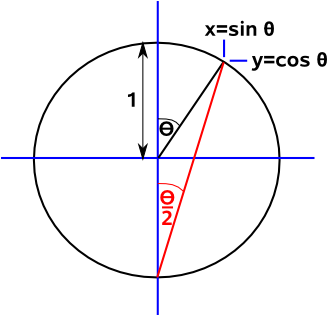
Graphical Representation We can show these relationships graphically where the angle is shown at the centre of a unit circle and the half angle is the angle at a point on the circumference. tan(θ)=opposite/adjacent = sin(θ)/(cos(θ)+1)

Derivation

In the above double angle formula we substitute t=2A to give:

1 - 2 sin²(t/2) = cos(t)

sin²(t/2) =0.5 (1- cos(t))

sin(t/2) =√(0.5 (1- cos(t)))

Similarly for cosine:

2 cos²(t/2) - 1 = cos(t)

2 cos²(t/2) = 1 + cos(t)

cos(t/2) =√(0.5 (1+ cos(t)))

EuclideanSpace

home

Hyperbola

Notes:

The graphical representation, on this page, for half angle formulae looks similar to the diagrams about stereographic projections on:

• this page
• and this page