Spherical coordinates allow points to be specified using one linear distances and two angles:
- r = radius (distance from axis of sphere)
- Latitude
- Longitude
This can be used to represent points on the surface of a sphere such as the earth as explained on this page.
Cartesian to Spherical Polar Coordinates
|
= |
|
Spherical Polar Coordinates to Cartesian
We can assign an arbitrary x,y,z coordinate system in the local frame of the earth:
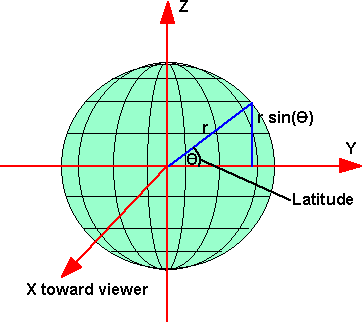
so from this diagram we can see that:
z = r sin(latitude)
and if we are on the Greenwich meridian then:
x = r cos(latitude)
but if we are not on the Greenwich meridian then this has to be modified depending on the latitude, so,
x = r cos(latitude) cos (longitude)
the y can be calculated from:
r2 = x2 + y2 + z2
therefore y = r *sqrt(1 - sin(latitude) - cos(latitude) cos (longitude))
|
= |
|

