Maths - Projections of lines on lines

We want to find the component of line A that is parallel to line B and the component of line A that is perpendicular to line B.

I also am planning to cover projections on planes here.

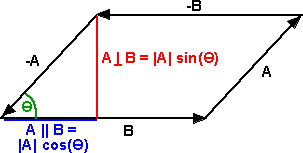
To do this we will use the following notation:

A || B = the component of line A that is parallel to line B.
A B = the component of line A that is perpendicular to line B and in the plane of both A and B..

We will also use:

|A| = the scalar magnitude of vector A.
= the angle between vector A and vector B
= a unit vector in the direction of A

So: = A / |A|

Relationship between these quantities

If we add the the parallel and perpendicular components then we get the original vector, which gives us the following equation:

A = A || B + A B

So if we have the perpendicular component we can work out the parallel component and visa-versa.

Calculation of the parallel component

From the above diagram, the scalar magnitude of the parallel component is |A| cos() and its direction is in the direction of vector B. So if we multiply |A| cos() by a unit vector along B, which is, B/|B|

So the vector we want is:

A || B = |A| cos() * B/|B|

We can use the vector dot product to calculate this, from this page we know that:

A•B = |A| |B| cos()

Therefore combining these equations gives:

A || B = A•B * B/|B|²

Calculation of the perpendicular component

From the above diagram, the scalar magnitude of the perpendicular component is |A| sin() and its direction is in the direction which is perpendicular to B and points toward A.

To find the direction that we want, first take a vector which is mutually perpendicular to A and B, this is given by the cross product A x B (which is out of the page on the above diagram). Now take a vector which is mutually perpendicular to this and vector B, this gives us the direction that we want.

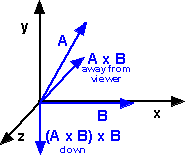
So the direction is:

-(A x B) x B

We need to normalise this, so a unit vector in the required direction is:

- x

From the diagram above the magnitude of the perpendicular is:

|A| sin()

So the perpendicular vector is:

A B =- |A| sin() x

But from this page we know that: x = sin() so:

A B = -|A| ( x ) x

but = A / |A| and = B / |B|

so:

A B = -(Ax B / |B|) x B / |B|

Alternative using Clifford or Geometric Algebra

For information about Clifford/Geometric Algebra see here.

So we have the following results for the component of line A that is parallel to line B and the component of line A that is perpendicular to line B:

A || B = A•B * B/|B|²
A B = (A x B) x B /|B|²

They both have this strange B/|B|² factor at the end, if we use geometric algebra division by a vector is valid (this gives a bivector) so we can use:

A || B = A•B / B
A B = (A x B) / B

As a check we have already said that A = A || B + A B so:

A = A•B / B + (A x B) / B

multiply both sides by B gives:

A * B = A•B + A x B

where * is a new type of multiplication used by Clifford/Geometric Algebra, this is the sum of the inner and outer products.

Alternative using Matrix representation

perpendicular component

A B = (A x B) x B/|B|²

A x B can be calculated as follows:

x = Ay * Bz - By * Az
y = Az * Bx - Bz * Ax
z = Ax * By - Bx * Ay

So,

(A B)x = ((Az * Bx - Bz * Ax) * Bz - By * (Ax * By - Bx * Ay)) / (Bx² + By² + Bz²)
(A B)y = ((Ax * By - Bx * Ay) * Bx - Bz * (Ay * Bz - By * Az)) / (Bx² + By² + Bz²)
(A B)z = ((Ay * Bz - By * Az) * By - Bx * (Az * Bx - Bz * Ax)) / (Bx² + By² + Bz²)

grouping terms,

(A B)x = (Az * Bx* Bz - Bz * Ax* Bz Ax * By* By + Bx * Ay* By) / (Bx² + By² + Bz²)
(A B)y = (Ax * By* Bx - Bx * Ay* Bx - Ay * Bz*Bz + By * Az*Bz) / (Bx² + By² + Bz²)
(A B)z = (Ay * Bz* By - By * Az* By - Az * Bx*Bx + Bz * Ax*Bx) / (Bx² + By² + Bz²)

In matrix form,

B) = 1 / (Bx² + By² + Bz²)*

-Bz* Bz- By* By	Bx * By	Bx* Bz
By* Bx	-BxBx- BzBz	By *Bz
Bz *Bx	Bz* By	-ByBy- BxBx

[A]

parallel component

A || P = A • P * P/|B|²

A • P can be calculated as follows:

Ax * Bx + Ay * By + Az * Bz

so,

(A || P)x = (Ax * Bx + Ay * By + Az * Bz) * Bx / (Bx² + By² + Bz²)
(A || P)y = (Ax * Bx + Ay * By + Az * Bz) * By/ (Bx² + By² + Bz²)
(A || P)z = (Ax * Bx + Ay * By + Az * Bz) * Bz/ (Bx² + By² + Bz²)

in matrix form this is:

(A || P) = 1 / (Bx² + By² + Bz²)*

Bx²	Bx * By	Bx * Bz
By * Bx	By²	By * Bz
Bz * Bx	Bz * By	Bz²

[A]

C++ Code

Thank you to minorlogic for the following code

// return projection v1 on to v2
inline vector3 projection( const vector3& v1, const vector3& v2 ) {
	float v2_ls = v2.len_squared();
	if( v2_ls > TINY ) {
		return v2 * ( dot( v2, v1 )/v2_ls );
	}else{
		return vector3(0,0,0);
   }
}

//------------------------------------------------------------------
// return orthogonal_component of v1 on v2
// i.e. the distance from v2 point to v1 line 
inline vector3 orthogonal_component( const vector3& v1, const vector3&  v2 ) {
	float v2_ls = v2.len_squared();
	if( v2_ls > TINY ) {
		return v1 - v2 * ( dot( v2, v1 )/v2_ls );
	}else{
		return vector3( 0, 0, 0);
   }
}

Example

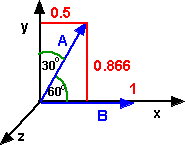
As an example we can take:

Vector A = unit length 30 degrees from y axis and 60 degrees from x axis

Vector B = unit length along x axis.

So just by looking at the diagram we can see that the component of A parallel to B = (0.5,0,0)

and the component of A perpendicular to B = (0,0.866,0)

we can now check this using the above formula:

A || B = A•B * B/|B|^{2 = 0.5}

and

A B = - (Ax B / |B|) x B / |B|

substitute A x B = - (0 , 0 , -0.866) and |B| = 1 gives and B=(1,0,0),

A B = -(0 , 0 , -0.866) x (1,0,0) = (0,0.866,0)

which are the expected results.

Skew Lines

So far we have only considered lines in 2 dimensions (or, at least, in the same plane).

When lines are in 3 dimensions it is possible that the lines do not intersect, being in two different planes.

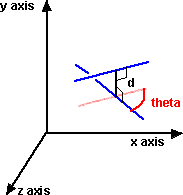
skew lines

We can use dual numbers to represent skew lines as explained here.

The relationship between the lines is represented by the dual number:

theta + d D

where:

theta is the angle between the lines (in radians)
d is the distance between the lines
D is the dual operator

if theta=0 then the lines are parallel

if d=0 then the lines intersect