Maths - Functions of a Complex Variable

Conformal Transformations

Transformations where the angle between two intersecting curves in Z plane equals the angle between corresponding curves in W plane.

A transformation is conformal where dw/dz ≠ 0 and the function is regular.

Differentiation

Is defined if dw/ dz is independent of angle.

In this case: dw/dz = dw/idy

therefore dv/dy - j du/dy = du/dx + j dv/dx

This gives the Cauchy Riemann equations:

dv/dy = du/dx

dv/dx = - du/dy

Harmonic Functions

∂u/∂x = ∂v/∂y —> ∂²u/∂x² = ∂v²/∂y∂x

∂u/∂y = -∂v/∂x —> ∂²u/∂y² = -∂v²/∂y∂x

therefore

∂²u/∂x² = -∂²u/∂y²

∂²u/∂x² + ∂²u/∂y² = 0

Therefore if a function obeys the Cauchy riemann equations then the real part is a harmonic function.

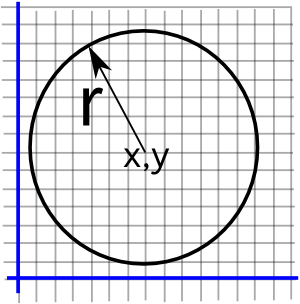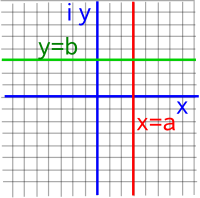
	(x - x1)² + (y - y1)² = r²	|z-d| = r
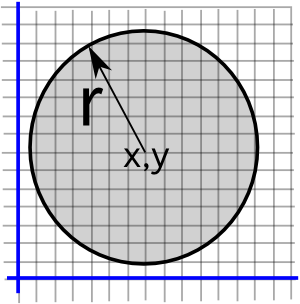	(x - x1)² + (y - y1)² < r²	|z-d| < r
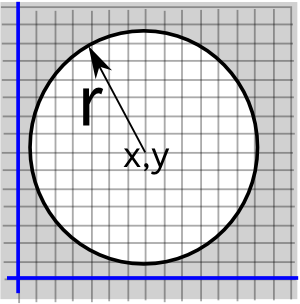	(x - x1)² + (y - y1)² > r²	|z-d| > r
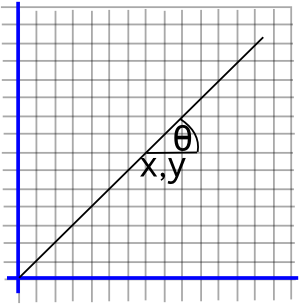	tan-1(y/x) = θ	arg(z)=θ

 

z plane		w plane
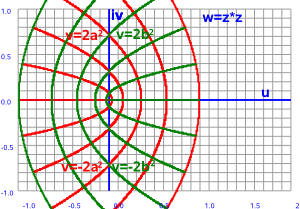
	--> w=z²
	--> w=ez
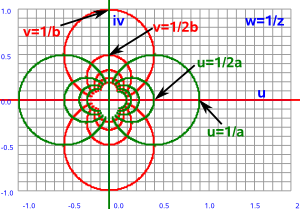
	--> w=1/z

Specific information about these functions is shown in the complex number part of the site (functions of a complex variable).

Cauchy's Theorem

If f(z) is analytic in a region R (no poles in R) then:

f(z) dz = 0

Extension of Cauchys Theorem

∫ round same singularities are equal.

∫ round several singularities = sum of ∫ round each singularity.

Use of Cauchys Theorem to evaluate Unknown Integral

e^-x² = √π

e^-x² cos(2 b x) dx = √π e^b²

e^-x² sin(2 b x) dx = 0

proof that:

e^-z² dz - > 0 as a - > ∞

principles used:

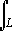1. | f(z) dz | <= 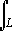| f(z) dz |
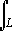2. |f(z) dz | = 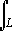| f(z)| |dz | <= ml

Poles of a function

A function can have several laurent series each corresponding to a pole:

Laurent Series:

f(z) = a_n/(z-a)ⁿ + a_n-1/(z-a)^n-1 + … +a₁/(z - a) + b₀ + b₁(z-a) + …

where:

• a = a pole of function
• a₁ = residue of pole

Evaluation of residue at simple pole

1. multiply by (z-pole)
2. take limit as z -> a

i.e. a₁ = lim_z->a(z - a) f(z)

Evaluation of residue at pole of order n

a₁ = 1/(n-1)! lim_z->a d^n-1/ d z^n-1{(z - a)ⁿ f(z)}

Application of poles: complex integration

f(z) d z = 2 π i (sum of enclosed resides)

Evaluation of integrals between ±∞

1. Find Poles
2. Take suitable path
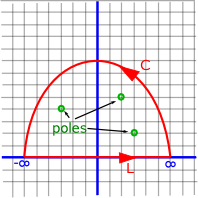
3. Find residues of poles inside path
4. Check if 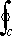=0 (denominator of f(z) 2 more than numerator) (proof uses 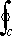≤ml)

 

Prerequisites

Complex numbers are discussed on this page and in particular functions of a complex variable are discussed here.

Calculus

Conformal Geometry

Projective Geometry

Linear Functions