Elaborator Reflection in Idris

Elaborator Reflection allows user to write meta-programs. These are programs which generate programs.

Idris uses a 'proof-theory-like' tactics language to convert Idris programs into a simpler type-theory known as TT syntax.

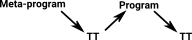Elaborator reflection allows this language to convert meta programs written by users into TT syntax.

For an embedded language example see this page.

TT syntax

Terms,
t ::= c   (constant)
| x       (variable)
| b.t     (binding)
| t t     (application)
| T       (type constructor)
| D       (data constructor)

Binders,
b::= λ x:t     (abstraction)
| let x->t :t   (let binding)
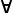|x :t      (function space)

Constants,
c::= Type_i          (type universes)
| i                 (integer literal)
| str               (string literal)

Vector Addition Example

This is an example, from the paper of how Idris is elaborated into TT.

Idris	TT
vAdd : Num a => Vect n a -> Vect n a -> Vect n a vAdd Nil Nil = Nil vAdd (x :: xs) (y :: ys) = x + y :: vAdd xs ys	vAdd : (a : Type)->(n:Nat)->Num a-> Vect n a->Vect n a->Vect n a var a:Type , c:Num a. vAdd a Z c (Nil a) (Nil a)->Nil a var a:Type , k:Nat , c:Num a, x:a , xs:Vect k a , y:a , ys:Vect k a. vAdd a (S k) c ((::) a k x xs) ((::) a k y ys) -> ((::) a k ((+) c x y) (vAdd a k c xs ys))

Idris

vAdd : Num a => Vect n a ->
          Vect n a -> Vect n a
vAdd Nil       Nil       = Nil
vAdd (x :: xs) (y :: ys) =
           x + y :: vAdd xs ys

vAdd : (a : Type)->(n:Nat)->Num a->
       Vect n a->Vect n a->Vect n a
var a:Type , c:Num a.
   vAdd a Z c (Nil a) (Nil a)->Nil a
var a:Type , k:Nat , c:Num a,
     x:a , xs:Vect k a , y:a , ys:Vect k a.
     vAdd a (S k) c ((::) a k x xs) ((::) a k y ys)
             -> ((::) a k ((+) c x y) (vAdd a k c xs ys))

Tactics

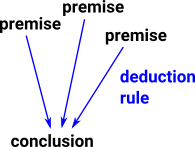
Forward Deduction

We sometimes think of a deduction rule as starting from a set of things we know (premises) and leading to something we wish to prove (conclusion).

Backward Deduction (Tactics)

When we are using a tactics system we start with what we want to prove (conclusion) and we go back to all the things we have to prove for that to be true (the premises).

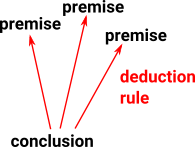So in a tactics system we start with a goal (conclusion), then we reduce this to a set of sub-goals and so on.

Proof Tree

The proof tree can hold the tree of goals and sub-goals encoded as proof objects.

The complete proof tree can hold a theorem (or by Curry-Howard a program).

In proof assistants the proof tree is constructed, from an incomplete tree, by filling in the holes (unknown terms).

The nodes can be encoded as λ-terms or a collection of tactic calls. However λ-terms are not very good at holding holes (open terms) because they require extra (outside proof) information.

Proof Monad

Add monadic structure to proof object to allow exra information to be held for holes.

https://github.com/idris-lang/Idris-dev/blob/master/libs/prelude/Language/Reflection/Elab.idr

A tactic is impemented by a function

TT -> List (TTName, TT) -> Tactic

where

The first argument is the goal type,
The second is the local proof context,
The return result

Proof State

A proof state is a tuple (see Brady 2013) consisting of the following:

A global context, C, containing pattern matching definitions and their types.
A local context, Δ, containing pattern bindings.
A proof term, e, in TT_dev
Unsolved unification problems, P
- These take the form ( Γ,e₁,e₂), i.e. the context in which the problem is to be solved, and the expressions to be unified.
A hole queue, Q.

Identity Proof

identity proof

see here

Idris Top Level

idris top level

Elab Monad

The Elab monad holds a proof state inside, which has:

A goal type
A proof term that is incrementally built up.
A hole queue
A collection of open unification problems
A supply of fresh names

The following is Idris code from module Language.Reflection.Elab which is in libs->prelude.

elab implementation

The state is really held in the Haskell code.

see

Module : Idris.Elab.Term
Description : Code to elaborate terms.

    -- | Do a step in the reflected elaborator monad. The input is the
    -- step, the output is the (reflected) term returned.
    runTacTm :: Term -> ElabD Term
    runTacTm tac@(unApply -> (P _ n _, args))
      | n == tacN "Prim__Solve"
      = do ~[] <- tacTmArgs 0 tac args -- patterns are irrefutable
           -- because `tacTmArgs` returns lists of exactly the size
           -- given to it as first argument
           solve
           returnUnit
      | n == tacN "Prim__Goal"
      = do ~[] <- tacTmArgs 0 tac args
           hs <- get_holes
<snip>

elab haskell

Elaborator Code

Running elaborator from within Idris environment:

idNat : Nat -> Nat
idNat = %runElab (do intro `{{x}}
                     fill (Var `{{x}})
                     solve)

This uses the %runElab e declaration.

'e' has the type Elab ()

It adds:

new type declation function
data type definitions

generated by the Elab action generated by e to the context.

Haskell Code:

elaborator haskell code

implementation

idris data types

https://koerbitz.me/posts/A-Look-at-the-Idris-Internals-Part-I-Overview-and-Parsing.html

idris tt

implementation

Idris> :browse Language.Reflection.Elab.Tactics
Namespaces:
  
Names:
  addImplementation : TTName -> TTName -> Elab ()
  apply : Raw -> List Bool -> Elab (List TTName)
  attack : Elab ()
  check : List (TTName, Binder TT) -> Raw -> Elab (TT, TT)
  claim : TTName -> Raw -> Elab ()
  compute : Elab ()
  converts : TT -> TT -> Elab ()
  convertsInEnv : List (TTName, Binder TT) -> TT -> TT -> Elab ()
  currentNamespace : Elab (List String)
  debug : Elab a
  debugMessage : List ErrorReportPart -> Elab a
  declareDatatype : TyDecl -> Elab ()
  declareType : TyDecl -> Elab ()
  defineDatatype : DataDefn -> Elab ()
  defineFunction : FunDefn Raw -> Elab ()
  fail : List ErrorReportPart -> Elab a
  fill : Raw -> Elab ()
  focus : TTName -> Elab ()
  forall : TTName -> Raw -> Elab ()
  gensym : String -> Elab TTName
  getEnv : Elab (List (TTName, Binder TT))
  getGoal : Elab (TTName, TT)
  getGuess : Elab TT
  getHoles : Elab (List TTName)
  getSourceLocation : Elab SourceLocation
  intro : TTName -> Elab ()
  intro' : Elab ()                                                                            
  isTCName : TTName -> Elab Bool                                                              
  letbind : TTName -> Raw -> Raw -> Elab ()                                                   
  lookupArgs : TTName -> Elab (List (TTName, List FunArg, Raw))                               
  lookupArgsExact : TTName -> Elab (TTName, List FunArg, Raw)                                 
  lookupDatatype : TTName -> Elab (List Datatype)                                             
  lookupDatatypeExact : TTName -> Elab Datatype                                               
  lookupFunDefn : TTName -> Elab (List (FunDefn TT))                                          
  lookupFunDefnExact : TTName -> Elab (FunDefn TT)                                            
  lookupTy : TTName -> Elab (List (TTName, NameType, TT))                                     
  lookupTyExact : TTName -> Elab (TTName, NameType, TT)                                       
  matchApply : Raw -> List Bool -> Elab (List TTName)                                         
  metavar : TTName -> Elab ()                                                                 
  normalise : List (TTName, Binder TT) -> TT -> Elab TT                                       
  operatorFixity : String -> Elab Fixity                                                      
  patbind : TTName -> Elab ()                                                                 
  patvar : TTName -> Elab ()                                                                  
  resolveTC : TTName -> Elab ()                                                               
  rewriteWith : Raw -> Elab ()                                                                
  runElab : Raw -> Elab () -> Elab (TT, TT)                                                   
  search : Elab ()                                                                            
  search' : Int -> List TTName -> Elab ()                                                     
  solve : Elab ()                                                                             
  sourceLocation : Elab ()                                                                    
  unfocus : TTName -> Elab ()                                                                 
  whnf : TT -> Elab TT                                                                        
Idris>

EuclideanSpace

home

Sources for this page:

Idris tutorial
Edwin Brady’s 2013 paper.
for customising the elaboration process see Elaborator reflection: extending Idris in Idris
and David Christiansen’s PhD thesis
Dependently Typed Functional Programs and their Proofs - McBride 1999
An Extended Calculus of Constructions - Zhaohui Luo

Epic:

For theory about converting one language into another see operational semantics theory.

Semantics

This page explains elaborator in Idris.

This page explains semantics.

See this website

Operational semantics describes the effect of each statement on the state – usually giving the post-state as a function of the pre-state.
Axiomatic Semantics usually defines a translation into logic formulae in some well defined logic language – the formulae describe, for each statement, the relation between the pre-state and the post-state of the executing the statement. This is usually given as a predicate transformer: a formula is true at the post-state if some syntactic transformation of it is true at the pre-state – or the other way around. Logic models are sometimes given over which these formulae are interpreted – the effect of a program in these models is the interpretation of the formulae – usually a relation.
Denotational semantics defines a translation into some (partial) function space usually defined in set/category theory. The meaning of a program is a (partial) function/relation in that space.

idris
Cadair Idris

Curry-Howard Correspondence

There is a relationship between computer programs and mathematical proofs, this is known as the Curry-Howard correspondence.

A type in λ-calculus has the same mathematical structure as a proposition in intuitionistic logic.

A constructor for that type corresponds to a proof of the proposition. The following table has some specific types with their corresponding propositions:

Proposition	Type
true formula	unit type
false formula	empty type
implication	function type
conjunction	product type
disjunction	sum type
universal quantification	generalised product type (Π type)
existential quantification	generalised sum type (Σ type)

For more information about the Curry-Howard correspondence see the page here.

metadata block

see also:	Idris tutorial Edwin Brady’s 2013 paper. Dependently Typed Functional Programs and their Proofs - McBride 1999 An Extended Calculus of Constructions - Zhaohui Luo
Correspondence about this page