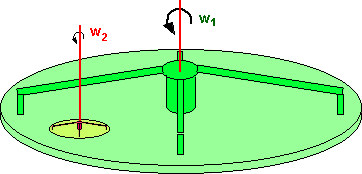
Imagine a rotating platform, this is rotating at w1 radians per second. On this platform, and offset by 1m from the centre, is a smaller rotating platform. This small platform is rotating at w2 radians per second relative to the large platform.
What is the angular velocity of the small platform relative to the earth?
The answer is that it is w1 + w2 radians per second.
Note: this is different from the planetary motion example in that the whole frame of reference is rotating.
However this example is relatively simple because the axis of rotation is in the same direction, so what happens if we rotate w2 by 45 degrees?
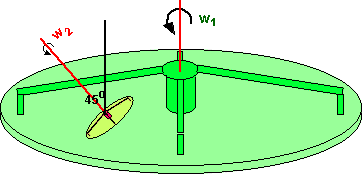
The smaller rotating platform now has a very complicated motion, I'm not sure we can represent its rotation by an equivalent single angular velocity? This example is made more complex by the translation which is also a function of time, perhaps we can remove that effect by putting the smaller rotating platform on the w1 axis as follows:
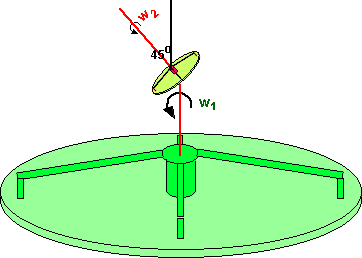
The smaller rotating platform still has a very complicated motion which does not appear to be represented by a single angular velocity. Perhaps the best way to analyze it is that the smaller rotating platform has a single angular velocity at any instant in time (w1 + w2), but this angular velocity is continuously varying with time. So angular momentum is continuously being changed in the system (so a closed system won't continue to rotate in this complex way).
Further Information
These pages contain examples to illustrate the principles involved, for an discussion of the theory about angular momentum see this page.




