Maths - 3D Rotations and Translations using multivectors

Prerequisites

You may want to review vectors:

Applying a multivector to a point

To calculate the rotated point from the original position of the point.

P2=m * P1 * m-1

 

In some sources I have seen this transform shown as:
A(b) =Ab(A#)-1

where:

a# = Main involution sumi(-1)ia<i&gt;

Such transformations satisfy A(b) |A(c) = b |c and are known as Lorentz transforms, or as isometries of inner product- |
If A is even then A(b) = AbA-1 and we have A(bc)) = A(b)A(c) .
If A is a k-versor then A# = (-1)kA so that A(bc) = (-1)kA(b)A(c).

 

If, m = m.e + m.ex + m.ey +m.ez + m.exy + m.ezx + m.eyz + m.exyz

and

m.e * m.exyz = m.ex *m.eyz + m.ey*m.ezx + m.ez*m.exy

and

1 = m.e2 - m.ex2 - m.ey2 - m.ez2 + m.exy2 + m.ezx2 + m.eyz2 - m.exyz2

then,

P1 * m-1 = (P1.x ,P1.y,P1.z)*( m.e -m.ex -m.ey -m.ez - m.exy - m.ezx - m.eyz + m.exyz)

which gives:

e = - P1.x * m.ex - P1.y * m.ey - P1.z * m.ez
ex = P1.x * m.e - P1.y * m.exy + P1.z * m.ezx
ey = P1.y * m.e + P1.x * m.exy - P1.z * m.eyz
ez = P1.z * m.e - P1.x * m.ezx + P1.y * m.eyz
exy = - P1.y * m.ex + P1.x * m.ey + P1.z * m.exyz
ezx = P1.z * m.ex - P1.x * m.ez + P1.y * m.exyz
eyz = - P1.z * m.ey + P1.y * m.ez + P1.x * m.exyz
exyz = - P1.z * m.exy - P1.y * m.ezx - P1.x * m.eyz

so m * P1 * m-1 gives,

e = m.e * (- P1.x * m.ex- P1.y * m.ey- P1.z * m.ez) + m.ex * (P1.x * m.e- P1.y * m.exy+ P1.z * m.ezx) + m.ey * (P1.y * m.e+ P1.x * m.exy- P1.z * m.eyz) + m.ez * (P1.z * m.e- P1.x * m.ezx+ P1.y * m.eyz) - m.exy * (- P1.y * m.ex+ P1.x * m.ey+ P1.z * m.exyz) - m.ezx * (P1.z * m.ex- P1.x * m.ez+ P1.y * m.exyz) - m.eyz * (- P1.z * m.ey+ P1.y * m.ez+ P1.x * m.exyz) - m.exyz * (- P1.z * m.exy- P1.y * m.ezx- P1.x * m.eyz)
ex = m.ex * (- P1.x * m.ex- P1.y * m.ey- P1.z * m.ez) + m.e * (P1.x * m.e- P1.y * m.exy+ P1.z * m.ezx) - m.exy * (P1.y * m.e+ P1.x * m.exy- P1.z * m.eyz) + m.ezx * (P1.z * m.e- P1.x * m.ezx+ P1.y * m.eyz) + m.ey * (- P1.y * m.ex+ P1.x * m.ey+ P1.z * m.exyz) - m.ez * (P1.z * m.ex- P1.x * m.ez+ P1.y * m.exyz) - m.exyz * (- P1.z * m.ey+ P1.y * m.ez+ P1.x * m.exyz) - m.eyz * (- P1.z * m.exy- P1.y * m.ezx- P1.x * m.eyz)
ey = m.ey * (- P1.x * m.ex- P1.y * m.ey- P1.z * m.ez) + m.exy * (P1.x * m.e- P1.y * m.exy+ P1.z * m.ezx) + m.e * (P1.y * m.e+ P1.x * m.exy- P1.z * m.eyz) - m.eyz * (P1.z * m.e- P1.x * m.ezx+ P1.y * m.eyz) - m.ex * (- P1.y * m.ex+ P1.x * m.ey+ P1.z * m.exyz) - m.exyz * (P1.z * m.ex- P1.x * m.ez+ P1.y * m.exyz) + m.ez * (- P1.z * m.ey+ P1.y * m.ez+ P1.x * m.exyz) - m.ezx * (- P1.z * m.exy- P1.y * m.ezx- P1.x * m.eyz)
ez = m.ez * (- P1.x * m.ex- P1.y * m.ey- P1.z * m.ez) - m.ezx * (P1.x * m.e- P1.y * m.exy+ P1.z * m.ezx) + m.eyz * (P1.y * m.e+ P1.x * m.exy- P1.z * m.eyz) + m.e * (P1.z * m.e- P1.x * m.ezx+ P1.y * m.eyz) - m.exyz * (- P1.y * m.ex+ P1.x * m.ey+ P1.z * m.exyz) + m.ex * (P1.z * m.ex- P1.x * m.ez+ P1.y * m.exyz) - m.ey * (- P1.z * m.ey+ P1.y * m.ez+ P1.x * m.exyz) - m.exy * (- P1.z * m.exy- P1.y * m.ezx- P1.x * m.eyz)
exy = m.exy * (- P1.x * m.ex- P1.y * m.ey- P1.z * m.ez) + m.ey * (P1.x * m.e- P1.y * m.exy+ P1.z * m.ezx) - m.ex * (P1.y * m.e+ P1.x * m.exy- P1.z * m.eyz) + m.exyz * (P1.z * m.e- P1.x * m.ezx+ P1.y * m.eyz) + m.e * (- P1.y * m.ex+ P1.x * m.ey+ P1.z * m.exyz) + m.eyz * (P1.z * m.ex- P1.x * m.ez+ P1.y * m.exyz) - m.ezx * (- P1.z * m.ey+ P1.y * m.ez+ P1.x * m.exyz) + m.ez * (- P1.z * m.exy- P1.y * m.ezx- P1.x * m.eyz)
ezx = m.ezx * (- P1.x * m.ex- P1.y * m.ey- P1.z * m.ez) - m.ez * (P1.x * m.e- P1.y * m.exy+ P1.z * m.ezx) + m.exyz * (P1.y * m.e+ P1.x * m.exy- P1.z * m.eyz) + m.ex * (P1.z * m.e- P1.x * m.ezx+ P1.y * m.eyz) - m.eyz * (- P1.y * m.ex+ P1.x * m.ey+ P1.z * m.exyz) + m.e * (P1.z * m.ex- P1.x * m.ez+ P1.y * m.exyz) + m.exy * (- P1.z * m.ey+ P1.y * m.ez+ P1.x * m.exyz) + m.ey * (- P1.z * m.exy- P1.y * m.ezx- P1.x * m.eyz)
eyz = m.eyz * (- P1.x * m.ex- P1.y * m.ey- P1.z * m.ez) + m.exyz * (P1.x * m.e- P1.y * m.exy+ P1.z * m.ezx) + m.ez * (P1.y * m.e+ P1.x * m.exy- P1.z * m.eyz) - m.ey * (P1.z * m.e- P1.x * m.ezx+ P1.y * m.eyz) + m.ezx * (- P1.y * m.ex+ P1.x * m.ey+ P1.z * m.exyz) - m.exy * (P1.z * m.ex- P1.x * m.ez+ P1.y * m.exyz) + m.e * (- P1.z * m.ey+ P1.y * m.ez+ P1.x * m.exyz) + m.ex * (- P1.z * m.exy- P1.y * m.ezx- P1.x * m.eyz)
exyz = m.exyz * (- P1.x * m.ex- P1.y * m.ey- P1.z * m.ez) + m.eyz * (P1.x * m.e- P1.y * m.exy+ P1.z * m.ezx) + m.ezx * (P1.y * m.e+ P1.x * m.exy- P1.z * m.eyz) + m.exy * (P1.z * m.e- P1.x * m.ezx+ P1.y * m.eyz) + m.ez * (- P1.y * m.ex+ P1.x * m.ey+ P1.z * m.exyz) + m.ey * (P1.z * m.ex- P1.x * m.ez+ P1.y * m.exyz) + m.ex * (- P1.z * m.ey+ P1.y * m.ez+ P1.x * m.exyz) + m.e * (- P1.z * m.exy- P1.y * m.ezx- P1.x * m.eyz)

 

e = m.e * (- P1.x * m.ex- P1.y * m.ey- P1.z * m.ez)+ m.ex * (P1.x * m.e- P1.y * m.exy+ P1.z * m.ezx)+ m.ey * (P1.y * m.e+ P1.x * m.exy- P1.z * m.eyz)+ m.ez * (P1.z * m.e- P1.x * m.ezx+ P1.y * m.eyz)- m.exy * (- P1.y * m.ex+ P1.x * m.ey+ P1.z * m.exyz)- m.ezx * (P1.z * m.ex- P1.x * m.ez+ P1.y * m.exyz)- m.eyz * (- P1.z * m.ey+ P1.y * m.ez+ P1.x * m.exyz)- m.exyz * (- P1.z * m.exy- P1.y * m.ezx- P1.x * m.eyz)
ex = m.ex * (- P1.x * m.ex- P1.y * m.ey- P1.z * m.ez)+ m.e * (P1.x * m.e- P1.y * m.exy+ P1.z * m.ezx)- m.exy * (P1.y * m.e+ P1.x * m.exy- P1.z * m.eyz)+ m.ezx * (P1.z * m.e- P1.x * m.ezx+ P1.y * m.eyz)+ m.ey * (- P1.y * m.ex+ P1.x * m.ey+ P1.z * m.exyz)- m.ez * (P1.z * m.ex- P1.x * m.ez+ P1.y * m.exyz)- m.exyz * (- P1.z * m.ey+ P1.y * m.ez+ P1.x * m.exyz)- m.eyz * (- P1.z * m.exy- P1.y * m.ezx- P1.x * m.eyz)
ey = m.ey * (- P1.x * m.ex- P1.y * m.ey- P1.z * m.ez)+ m.exy * (P1.x * m.e- P1.y * m.exy+ P1.z * m.ezx)+ m.e * (P1.y * m.e+ P1.x * m.exy- P1.z * m.eyz)- m.eyz * (P1.z * m.e- P1.x * m.ezx+ P1.y * m.eyz)- m.ex * (- P1.y * m.ex+ P1.x * m.ey+ P1.z * m.exyz)- m.exyz * (P1.z * m.ex- P1.x * m.ez+ P1.y * m.exyz)+ m.ez * (- P1.z * m.ey+ P1.y * m.ez+ P1.x * m.exyz)- m.ezx * (- P1.z * m.exy- P1.y * m.ezx- P1.x * m.eyz)
ez = m.ez * (- P1.x * m.ex- P1.y * m.ey- P1.z * m.ez)- m.ezx * (P1.x * m.e- P1.y * m.exy+ P1.z * m.ezx)+ m.eyz * (P1.y * m.e+ P1.x * m.exy- P1.z * m.eyz)+ m.e * (P1.z * m.e- P1.x * m.ezx+ P1.y * m.eyz)- m.exyz * (- P1.y * m.ex+ P1.x * m.ey+ P1.z * m.exyz)+ m.ex * (P1.z * m.ex- P1.x * m.ez+ P1.y * m.exyz)- m.ey * (- P1.z * m.ey+ P1.y * m.ez+ P1.x * m.exyz)- m.exy * (- P1.z * m.exy- P1.y * m.ezx- P1.x * m.eyz)
exy = m.exy * (- P1.x * m.ex- P1.y * m.ey- P1.z * m.ez)+ m.ey * (P1.x * m.e- P1.y * m.exy+ P1.z * m.ezx)- m.ex * (P1.y * m.e+ P1.x * m.exy- P1.z * m.eyz)+ m.exyz * (P1.z * m.e- P1.x * m.ezx+ P1.y * m.eyz)+ m.e * (- P1.y * m.ex+ P1.x * m.ey+ P1.z * m.exyz)+ m.eyz * (P1.z * m.ex- P1.x * m.ez+ P1.y * m.exyz)- m.ezx * (- P1.z * m.ey+ P1.y * m.ez+ P1.x * m.exyz)+ m.ez * (- P1.z * m.exy- P1.y * m.ezx- P1.x * m.eyz)
ezx = m.ezx * (- P1.x * m.ex- P1.y * m.ey- P1.z * m.ez)- m.ez * (P1.x * m.e- P1.y * m.exy+ P1.z * m.ezx)+ m.exyz * (P1.y * m.e+ P1.x * m.exy- P1.z * m.eyz)+ m.ex * (P1.z * m.e- P1.x * m.ezx+ P1.y * m.eyz)- m.eyz * (- P1.y * m.ex+ P1.x * m.ey+ P1.z * m.exyz)+ m.e * (P1.z * m.ex- P1.x * m.ez+ P1.y * m.exyz)+ m.exy * (- P1.z * m.ey+ P1.y * m.ez+ P1.x * m.exyz)+ m.ey * (- P1.z * m.exy- P1.y * m.ezx- P1.x * m.eyz)
eyz = m.eyz * (- P1.x * m.ex- P1.y * m.ey- P1.z * m.ez)+ m.exyz * (P1.x * m.e- P1.y * m.exy+ P1.z * m.ezx)+ m.ez * (P1.y * m.e+ P1.x * m.exy- P1.z * m.eyz)- m.ey * (P1.z * m.e- P1.x * m.ezx+ P1.y * m.eyz)+ m.ezx * (- P1.y * m.ex+ P1.x * m.ey+ P1.z * m.exyz)- m.exy * (P1.z * m.ex- P1.x * m.ez+ P1.y * m.exyz)+ m.e * (- P1.z * m.ey+ P1.y * m.ez+ P1.x * m.exyz)+ m.ex * (- P1.z * m.exy- P1.y * m.ezx- P1.x * m.eyz)
exyz = m.exyz * (- P1.x * m.ex- P1.y * m.ey- P1.z * m.ez)+ m.eyz * (P1.x * m.e- P1.y * m.exy+ P1.z * m.ezx)+ m.ezx * (P1.y * m.e+ P1.x * m.exy- P1.z * m.eyz)+ m.exy * (P1.z * m.e- P1.x * m.ezx+ P1.y * m.eyz)+ m.ez * (- P1.y * m.ex+ P1.x * m.ey+ P1.z * m.exyz)+ m.ey * (P1.z * m.ex- P1.x * m.ez+ P1.y * m.exyz)+ m.ex * (- P1.z * m.ey+ P1.y * m.ez+ P1.x * m.exyz)+ m.e * (- P1.z * m.exy- P1.y * m.ezx- P1.x * m.eyz)

 

e =

P1.x (-m.e * m.ex + m.e * m.ex + m.ey*m.exy - m.ez*m.ezx - m.exy*m.ey + m.ezx*m.ez - m.eyz* m.exyz+ m.exyz* m.eyz)
P1.y (-m.e* m.ey - m.ex* m.exy+ m.ey* m.e+ m.ez* m.eyz+ m.exy* m.ex- m.ezx* m.exyz- m.eyz* m.ez+ m.exyz* m.ezx)
P1.z (-m.e * m.ez+ m.ex * m.ezx- m.ey * m.eyz+ m.ez * m.e- m.exy * m.exyz- m.ezx * m.ex+ m.eyz * m.ey+ m.exyz *m.exy)
ex =

P1.x (-m.ex* m.ex+ m.e* m.e - m.exy* m.exy - m.ezx* m.ezx + m.ey* m.ey+ m.ez* m.ez- m.exyz * m.exyz+ m.eyz* m.eyz)
P1.y (-m.ex* m.ey- m.e* m.exy - m.exy* m.e + m.ezx* m.eyz - m.ey* m.ex- m.ez* m.exyz- m.exyz * m.ez+ m.eyz* m.ezx)
P1.z (-m.ex* m.ez+ m.e* m.ezx + m.exy* m.eyz + m.ezx* m.e + m.ey* m.exyz- m.ez* m.ex+ m.exyz * m.ey+ m.eyz* m.exy)
ey =

P1.x (-m.ey* m.ex + m.exy* m.e + m.e* m.exy+ m.eyz* m.ezx - m.ex* m.ey+ m.exyz* m.ez+ m.ez* m.exyz + m.ezx* m.eyz)
P1.y (-m.ey* m.ey - m.exy* m.exy + m.e* m.e- m.eyz* m.eyz + m.ex* m.ex- m.exyz* m.exyz+ m.ez* m.ez + m.ezx* m.ezx)
P1.z (-m.ey* m.ez + m.exy * m.ezx - m.e* m.eyz- m.eyz* m.e - m.ex* m.exyz- m.exyz* m.ex- m.ez* m.ey + m.ezx* m.exy)
ez =

P1.x (-m.ez* m.ex- m.ezx* m.e + m.eyz* m.exy - m.e* m.ezx- m.exyz* m.ey- m.ex* m.ez- m.ey* m.exyz+ m.exy* m.eyz)
P1.y (-m.ez* m.ey+ m.ezx* m.exy + m.eyz* m.e + m.e* m.eyz+ m.exyz* m.ex+ m.ex* m.exyz- m.ey* m.ez+ m.exy* m.ezx)
P1.z (-m.ez* m.ez- m.ezx* m.ezx - m.eyz* m.eyz + m.e* m.e- m.exyz* m.exyz+ m.ex* m.ex+ m.ey* m.ey+ m.exy* m.exy)
exy =

P1.x (-m.exy* m.ex + m.ey* m.e- m.ex* m.exy- m.exyz* m.ezx+ m.e* m.ey- m.eyz* m.ez- m.ezx* m.exyz - m.ez* m.eyz)
P1.y (-m.exy* m.ey - m.ey* m.exy- m.ex* m.e+ m.exyz* m.eyz- m.e* m.ex+ m.eyz* m.exyz- m.ezx* m.ez - m.ez* m.ezx)
P1.z (-m.exy* m.ez + m.ey* m.ezx+ m.ex* m.eyz+ m.exyz* m.e+ m.e* m.exyz+ m.eyz* m.ex+ m.ezx* m.ey - m.ez* m.exy)
ezx =

P1.x (-m.ezx* m.ex- m.ez* m.e+ m.exyz* m.exy- m.ex* m.ezx- m.eyz* m.ey- m.e* m.ez + m.exy* m.exyz- m.ey* m.eyz)
P1.y (-m.ezx* m.ey+ m.ez* m.exy+ m.exyz* m.e+ m.ex* m.eyz+ m.eyz* m.ex+ m.e* m.exyz + m.exy* m.ez- m.ey* m.ezx)
P1.z (-m.ezx* m.ez- m.ez* m.ezx- m.exyz* m.eyz+ m.ex* m.e- m.eyz* m.exyz+ m.e* m.ex - m.exy* m.ey- m.ey* m.exy)
eyz =

P1.x (-m.eyz* m.ex+ m.exyz* m.e+ m.ez * m.exy+ m.ey* m.ezx+ m.ezx* m.ey+ m.exy* m.ez + m.e* m.exyz - m.ex* m.eyz)
P1.y (-m.eyz* m.ey- m.exyz* m.exy+ m.ez* m.e- m.ey* m.eyz- m.ezx* m.ex- m.exy* m.exyz + m.e* m.ez - m.ex* m.ezx)
P1.z (-m.eyz* m.ez+ m.exyz* m.ezx- m.ez* m.eyz- m.ey* m.e+ m.ezx* m.exyz- m.exy* m.ex - m.e* m.ey - m.ex* m.exy)
exyz =

P1.x (-m.exyz* m.ex+ m.eyz* m.e+ m.ezx* m.exy- m.exy* m.ezx+ m.ez* m.ey- m.ey* m.ez+ m.ex* m.exyz- m.e* m.eyz)
P1.y (-m.exyz* m.ey- m.eyz* m.exy+ m.ezx* m.e+ m.exy* m.eyz- m.ez * m.ex+ m.ey* m.exyz+ m.ex* m.ez- m.e* m.ezx)
P1.z (-m.exyz* m.ez+ m.eyz* m.ezx- m.ezx* m.eyz+ m.exy* m.e+ m.ez* m.exyz+ m.ey* m.ex- m.ex* m.ey- m.e* m.exy)

cancel out any equal and opposite terms:

e =

0
ex =

P1.x (-m.ex* m.ex+ m.e* m.e - m.exy* m.exy - m.ezx* m.ezx + m.ey* m.ey+ m.ez* m.ez- m.exyz * m.exyz+ m.eyz* m.eyz)
P1.y (-2*m.ex* m.ey - 2*m.e* m.exy + 2*m.ezx* m.eyz - 2*m.ez* m.exyz)
P1.z (-2*m.ex* m.ez + 2*m.e* m.ezx + 2*m.exy* m.eyz + 2*m.ey* m.exyz)
ey = P1.x (-2*m.ey* m.ex +2* m.exy* m.e + 2*m.eyz* m.ezx + 2*m.exyz* m.ez)
P1.y (-m.ey* m.ey - m.exy* m.exy + m.e* m.e- m.eyz* m.eyz + m.ex* m.ex- m.exyz* m.exyz+ m.ez* m.ez + m.ezx* m.ezx)
P1.z (-2*m.ey* m.ez + 2*m.exy * m.ezx - 2*m.e* m.eyz - 2*m.ex* m.exyz)
ez = P1.x (-2*m.ez* m.ex- 2*m.ezx* m.e + 2*m.eyz* m.exy - 2*m.exyz* m.ey)
P1.y (-2*m.ez* m.ey+ 2*m.ezx* m.exy + 2*m.eyz* m.e + 2*m.exyz* m.ex)
P1.z (-m.ez* m.ez- m.ezx* m.ezx - m.eyz* m.eyz + m.e* m.e- m.exyz* m.exyz+ m.ex* m.ex+ m.ey* m.ey+ m.exy* m.exy)
exy = P1.x (-2*m.exy* m.ex + 2*m.ey* m.e- 2*m.exyz* m.ezx- 2*m.eyz* m.ez)
P1.y (-2*m.exy* m.ey - 2*m.ex* m.e+ 2*m.exyz* m.eyz- 2*m.ezx* m.ez)
P1.z (-2*m.exy* m.ez + 2*m.ey* m.ezx+ 2*m.ex* m.eyz+ 2*m.exyz* m.e)
ezx = P1.x (-2*m.ezx* m.ex- 2*m.ez* m.e+ 2*m.exyz* m.exy- 2*m.eyz* m.ey)
P1.y (-2*m.ezx* m.ey+ 2*m.ez* m.exy+ 2*m.exyz* m.e+ 2*m.ex* m.eyz)
P1.z (-2*m.ezx* m.ez- 2*m.exyz* m.eyz+ 2*m.ex* m.e - 2*m.exy* m.ey)
eyz = P1.x (-2*m.eyz* m.ex+2* m.exyz* m.e+ 2*m.ez * m.exy+ 2*m.ey* m.ezx)
P1.y (-2*m.eyz* m.ey- 2*m.exyz* m.exy+ 2*m.ez* m.e- 2*m.ezx* m.ex)
P1.z (-2*m.eyz* m.ez+ 2*m.exyz* m.ezx- 2*m.ey* m.e- 2*m.exy* m.ex)
exyz = 0

putting this in rows and columns gives:

  P1.x P1.y P1.z
ex -m.ex2+ m.e2 - m.exy2 - m.ezx2 + m.ey2+ m.ez2- m.exyz2+ m.eyz2 -2*m.ex* m.ey - 2*m.e* m.exy + 2*m.ezx* m.eyz - 2*m.ez* m.exyz -2*m.ex* m.ez + 2*m.e* m.ezx + 2*m.exy* m.eyz + 2*m.ey* m.exyz
ey -2*m.ey* m.ex +2* m.exy* m.e + 2*m.eyz* m.ezx + 2*m.exyz* m.ez -m.ey2 - m.exy2 + m.e2- m.eyz2 + m.ex2- m.exyz2 + m.ez2 + m.ezx2 -2*m.ey* m.ez + 2*m.exy * m.ezx - 2*m.e* m.eyz - 2*m.ex* m.exyz
ez -2*m.ez* m.ex- 2*m.ezx* m.e + 2*m.eyz* m.exy - 2*m.exyz* m.ey -2*m.ez* m.ey+ 2*m.ezx* m.exy + 2*m.eyz* m.e + 2*m.exyz* m.ex -m.ez2- m.ezx2 - m.eyz2 + m.e2- m.exyz2+ m.ex2+ m.ey2+ m.exy2
exy -2*m.exy* m.ex + 2*m.ey* m.e- 2*m.exyz* m.ezx- 2*m.eyz* m.ez -2*m.exy* m.ey - 2*m.ex* m.e+ 2*m.exyz* m.eyz- 2*m.ezx* m.ez -2*m.exy* m.ez + 2*m.ey* m.ezx+ 2*m.ex* m.eyz+ 2*m.exyz* m.e
ezx -2*m.ezx* m.ex- 2*m.ez* m.e+ 2*m.exyz* m.exy- 2*m.eyz* m.ey -2*m.ezx* m.ey+ 2*m.ez* m.exy+ 2*m.exyz* m.e+ 2*m.ex* m.eyz -2*m.ezx* m.ez- 2*m.exyz* m.eyz+ 2*m.ex* m.e - 2*m.exy* m.ey
eyz -2*m.eyz* m.ex+2* m.exyz* m.e+ 2*m.ez * m.exy+ 2*m.ey* m.ezx -2*m.eyz* m.ey- 2*m.exyz* m.exy+ 2*m.ez* m.e- 2*m.ezx* m.ex -2*m.eyz* m.ez+ 2*m.exyz* m.ezx- 2*m.ey* m.e- 2*m.exy* m.ex

The values in red correspond to the quaternion equivalents below:

The equivilant equation for rotating a point using a quaternion is:

sfvec3d transform(sfvec3d p1){
	sfvec3d p2 = new sfvec3f();
	p2.x = w*w*p1.x + 2*y*w*p1.z - 2*z*w*p1.y + x*x*p1.x + 2*y*x*p1.y + 2*z*x*p1.z - z*z*p1.x - y*y*p1.x;
	p2.y = 2*x*y*p1.x + y*y*p1.y + 2*z*y*p1.z + 2*w*z*p1.x - z*z*p1.y + w*w*p1.y - 2*x*w*p1.z - x*x*p1.y;
	p2.z = 2*x*z*p1.x + 2*y*z*p1.y + z*z*p1.z - 2*w*y*p1.x - y*y*p1.z + 2*w*x*p1.y - x*x*p1.z + w*w*p1.z;
	return p2;
}

putting this in rows and columns gives:

  P1.x P1.y P1.z
x w*w+ x*x- z*z - y*y + 2*y*x - 2*z*w 2*y*w+ 2*z*x
y 2*x*y+ 2*w*z y*y- z*z+ w*w- x*x 2*z*y- 2*x*w
z 2*x*z- 2*w*y 2*y*z+ 2*w*x z*z- y*y- x*x+ w*w


Rotation

rotation

Use of multivector to represent pure rotation.

axis

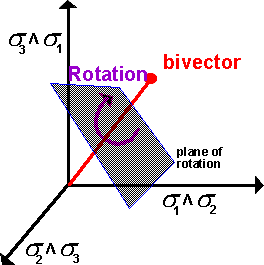
A multivector can be used to represent a rotation in 3 dimensions. If we are rotating through t radians about a unit vector (x1,y1,z1) then the rotation can be represented by multiplying by the following multivector:

multivector = cos(t/2) + σ1 outer product σ2 ( x1 * sin(t/2)) + σ3 outer product σ1 (y1 * sin(t/2)) + σ2 outer product σ3 ( z1 * sin(t/2))

 

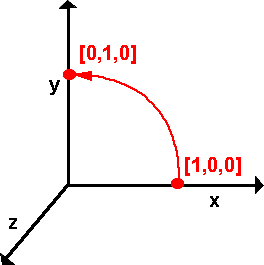
Example 1

As an example of using quaternions for 3D rotations, what is the quaternion to represent a 90 degree (PI/2 radian) rotation about the z axis:

example 1

q = cos(t/2) + σ1 outer product σ2 ( x1 * sin(t/2)) + σ3 outer product σ1 (y1 * sin(t/2)) + σ2 outer product σ3 ( z1 * sin(t/2))

= 0.7071 + σ1 outer product σ2 * 0 + σ3 outer product σ1 * 0 + σ2 outer product σ3 * 0.7071

So how can we use this to show that point [1,0,0] will be rotated to [0,1,0]

let us represent the point [1,0,0] by the quaternion 0 + σ1 outer product σ2 1 + σ3 outer product σ1 0 + σ2 outer product σ3 0

Then apply the quaternion q as follows:

P2=m * P1 * m-1

=(0.7071 + k 0.7071)*( σ1 outer product σ2 1)*(0.7071 - σ2 outer product σ3 0.7071)

multiplying out the first two quaternions first gives,

=(σ1 outer product σ2 0.7071 + (σ2 outer product σ3*σ1 outer product σ2)0.7071)*(0.7071 - σ2 outer product σ3 0.7071)

=(σ1 outer product σ2 0.7071 + σ3 outer product σ1 0.7071)*(0.7071 - σ2 outer product σ3 0.7071)

then multiply the remaining quaternions,

=σ1 outer product σ2 * 0.5 + σ3 outer product σ1 0.5 + σ3 outer product σ1 0.5 - σ1 outer product σ2 * 0.5

=σ3 outer product σ1

which converts to the point [0,1,0] as required.

 

Interpolating Rotations

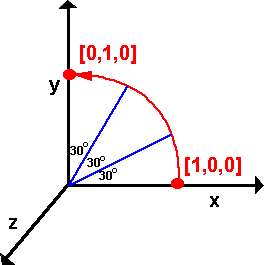
Quaternions can be used to interpolate points when an object is rotating.

Example 2

Let us take the 90 degree rotation in example 1 and calculate two interpolated points.

example 2

Since the angles are simple we can calculate the result from q = cos(t/2) + σ1 outer product σ2 ( x1 * sin(t/2)) + σ3 outer product σ1 (y1 * sin(t/2)) + σ2 outer product σ3 ( z1 * sin(t/2))

So the quaternions represented the two interpolated points are:

q1 = 0.966 + σ1 outer product σ2 0 + σ3 outer product σ1 0 + σ2 outer product σ3 0.259

q2 = 0.866 + σ1 outer product σ2 0 + σ3 outer product σ1 0 + σ2 outer product σ3 0.5
metadata block
see also:

 
Correspondence about this page

Book Shop - Further reading.

Where I can, I have put links to Amazon for books that are relevant to the subject, click on the appropriate country flag to get more details of the book or to buy it from them.
flag flag flag flag flag flag Clifford Algebra to Geometric Calculus: A Unified Language for Mathematics and Physics (Fundamental Theories of Physics). This book is intended for mathematicians and physicists rather than programmers, it is very theoretical. It covers the algebra and calculus of multivectors of any dimension and is not specific to 3D modelling.

 

Terminology and Notation

Specific to this page here:

 

This site may have errors. Don't use for critical systems.

Copyright (c) 1998-2023 Martin John Baker - All rights reserved - privacy policy.