A ball is hit by cue on the left, if we assume that the momentum is transferred only as an impulse, how do we work out the resulting linear and angular velocity of the ball?

Assume the following:
- impulse = 1 kg m/s
- mass of ball = 1 kg
- radius of ball = r = 50 cm
- offset of cue = 2/5 r2 (chosen in hope of simplifying calculations, because this is the moment of inertia)
Method 1
linear velocity = impulse / mass = 1 m/s in the direction of the impulse
angular velocity = offset * impulse / I = (2/5 r2)/(2/5 r2) = 1 rad/sec clockwise
Method 2
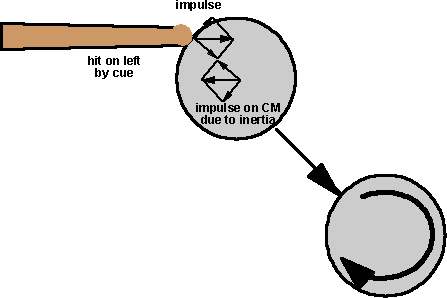
In this method the impulse is resolved into a component toward the centre of mass and a component at 90 degrees, then assume that the component toward the CM generates the linear velocity and the component at 90 degrees generates the angular velocity.
Which is correct?
Can anyone help me here?
I think method 1 is correct because there is no justification for saying that the component toward the CM generates only the linear velocity and the component at 90 degrees generates only the angular velocity. However method 1 does not seem intuitively right, it seems that there should be some linear component to the right.
This is not a closed system so we cant use the conservation of angular momentum, is there a similar example which is a closed system, so that we can use conservation of angular momentum to check the result?